Златното Сечение в Изкуството и Дизайна: Основни принципи и Приложения

Как да въведем Златното сечение в своите проекти за постигане на перфектен баланс и хармония? В тази статия ще ви покажем нагледно ключовите принципи и ще ви даде практически съвети как да го използвате. 

Ще откриете съвети и трикове за успешно приложение на Златното Сечение в графичния и уебдизайн. Стратегии за постигане на въздействащи визуални резултати и по-добро потребителско изживяване на подсъзнателно ниво.

След като откриете тайните на Златното Сечение може да превърнете графичните си изображения в истинско произведение на изкуството. Съвети, инспирация (вдъхновение) и практически ръководства за създаване на въздействащи, хармонични дизайни!

1. Какво е Златното сечение и какво представлява математически?
2. Кои са основните характеристики и свойства на Златното сечение?
3. Как Златното сечение е присъствало в различни култури и периоди на историята?
4. Как се използва Златното сечение в графичния дизайн и уебдизайна?
5. Кои са примерите за приложение на Златното сечение в архитектурата?
6. Как Златното сечение се използва в изкуството и какво влияние има върху визуалното възприятие?
7. Как Златното сечение се изразява в природата и какви са примерите за това?
8. Как дизайнерите и художниците използват Златното сечение за постигане на визуален баланс и хармония?
   
   

В достигналата до нас антична литература Златното сечение се среща за първи път в произведението „Елементи“ на Евклид. 

Дефиниция на Златното сечение и история на неговото откриване

 

Златно сечение е известно също като Златна пропорция, Златен коефициент или божествената пропорция) е ирационално число в математиката, което изразява съотношение на части, за които по-голямата част се отнася към по-малката така, както цялото към по-голямата. То се отбелязва с гръцката буква φ и има стойност приблизително равна на 1,618.

 

Значение в математиката и приложения в различни области

Златното сечение във времето

 

Принцип, формулиран от гръцкия философ Протагор и принципът на Златното сечение, благодарение на който се получава максимално чувство за красота, изграждащо най-съвършеното творение на природата - човешкото тяло. 

 

Според Протагор: “Човекът е мярка на съществуващите неща, заради което те съществуват, и на несъществуващите, за това те не съществуват.”

 

Според Демокрит мярката е норма на чувственото възприятие. Тя е свързана с прекрасното, с насладата и удоволствието. 

 

Според Платон, мярката е универсален принцип – тя е резултат от измерение, това е съответствието на вещта на нейното предназначение. 

 

Според Аристотел мярката е неделима и единна – “това е всичко, което е неделимо по качество и по количество”. “Най-главните форми на прекрасното - това са порядъкът, съразмерността и определеността.”

Златното сечение, известно още като Божествено деление или просто φ (фи), има дълга история, обхващаща различни периоди и култури.

 

 

1. Древен Египет:

• Първите записи за Златното сечение се намират в древен Египет, където фараоните и архитектите използвали пропорции, близки до тези на Златното сечение, при строежа на пирамидите и други сгради.

 

 

2. Древна Гърция:

•   Гръцките математици, особено Евклид и Птолемей, допринесли за разбирането на Златното сечение.
•   Фибоначиевата последователност, която води до Златното сечение, била открита и изследвана.

 

3. Средновековие и Ренесанс:

• Знанията за Златното сечение били запазени през средновековието от арабските математици и трансмитирани обратно в Европа.
• В Ренесанса Златното сечение получава ново внимание, особено благодарение на трудовете на италианския математик Фибоначи и художника Леонардо да Винчи.

 

4. 18-19 век:

• Математици като Лагранж и Лаплас изследват свойствата на Златното сечение и свързват го със златното правоъгълник.
• Златното сечение става предмет на интерес и в архитектурата през този период.

 

5. 20 век:

•  Златното сечение се използва в модерното изкуство, дизайн и архитектура.
•  В науката, фракталите и хаос теорията разширяват разбирането за Златното сечение.

Кой е Фибоначи и какво е Числото на Фибоначи?

 

Фибоначи (Leonardo Fibonacci) е средновековен италиански математик от XIII век, наричан още Леонардо от Пиза (Leonardo of Pisa). Той е известен с въвеждането на Фибоначиевата последователност в европейската математика.

 

 

Редицата на Фибоначи е ред от числа, където всяко число е сумата на предишните две: 0, 1, 1, 2, 3, 5, 8, 13, 21 и така нататък. Това има много интересни свойства и се използва в различни математически и приложни области, включително в изчислителната математика, финансите и дори в ботаниката.

 

Числата на Фибоначи са описани за първи път в индийската математика още през 200 г. пр. н. е. в работата на Пингала за изброяване на възможни модели на санскритска поезия. 

 

Те са кръстени на италианския математик Леонардо от Пиза, известен също като Фибоначи, който въвежда последователността в западноевропейската математика в своята книга от 1202 г. Liber Abaci.

 

Според Wikipedia: Числата на Фибоначи се появяват неочаквано често в математиката, дотолкова, че има цяло списание, посветено на тяхното изследване, Fibonacci Quarterly. Приложенията на числата на Фибоначи включват компютърни алгоритми като техниката за търсене на Фибоначи и структурата на данните на купчината на Фибоначи и графики, наречени кубове на Фибоначи, използвани за свързване на паралелни и разпределени системи. Те също се появяват в биологични условия, като разклоняване на дървета, подреждане на листата върху стъблото, плодови кълнове на ананас, цъфтеж на артишок и подреждане на прицветниците на борова шишарка, въпреки че не се срещат във всички видове.

 

Числата на Фибоначи също са тясно свързани със златното сечение: формулата на Бине изразява n-то число на Фибоначи по отношение на n и златното сечение и предполага, че съотношението на две последователни числа на Фибоначи клони към златното сечение, когато n нараства. Числата на Фибоначи също са тясно свързани с числата на Лукас, които се подчиняват на същата рекурентна връзка и с числата на Фибоначи образуват допълваща се двойка последователности на Лукас.

 

Всъщност алгоритъмът за образуване на поредното число от редицата на Фибоначи изразява факта, че следствието (последното число от реда) зависи от предисторията (причините) по конкретния за тази редица начин, а именно: последното число е сума от двете предходни числа. Така този алгоритъм се включва в категорията на т. нар. рекурентни формули. Доколко с алгоритъма на 'златното сечение' могат да се обяснят природни и човешки феномени зависи именно от това, доколко тези феномени се подчиняват на горната проста и същевременно съответстваща добре на 'здравия разум' рекурентна зависимост на следствието от причините, които го пораждат. До Фибоначи основните алгоритми за описване на възпроизвеждащи формули са били аритметичната и геометричната прогресия. 

Днес Златното сечение продължава да бъде използвано и вдъхновява творци и учени в различни области. То представлява уникална комбинация от математика, изкуство и природа, което продължава да вълнува и вдъхновява хората.

Математически аспекти на Златното сечение:

•    Обяснение на фибоначиевото число и формулите, свързани с него.
•    Примери за как Златното сечение се изразява в различни математически конструкции.

 

 

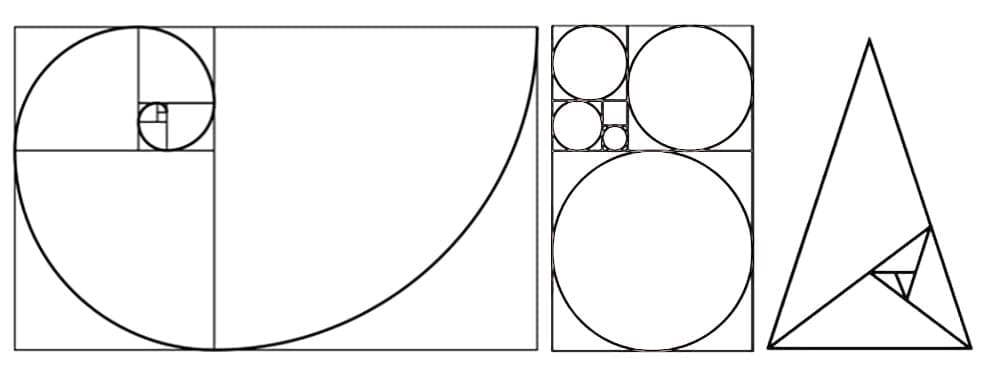
Геометрия на Златното сечение:

•    Как Златното сечение се използва в геометрията и конструкцията на златното правоъгълник.
•    Графично представяне на Златното сечение в контекста на различни фигури.

 

 

Приложения в изкуството:

•    Как художници използват Златното сечение в своите произведения.
•    Примери от историята на изкуствата, където този пропорция е била използвана.

Неостаряващи прочути шедьоври останали във времето в съответствие със Златното сечение са:

 

• Портретът на Мона Лиза, още нарична Джокондата е нарисувана от Леонардо Да Винчи през XVI век 
• Прочутата картиина на Вермеер "Момичето с перлената обеца"
• Витрувианският човек на Леонардо Да Винчи с пропорциите на човешкото тяло също са в унисон със Златното сечение. Скицата, нарисувана през 1490 г. е нарчана Закона на Пропорциите на човешкото тяло.  

 

 

 

 

 

Златното сечение в архитектурата:

•    Примери за архитектурни творения, които следват Златното сечение са Акрополът в Гърция, Египетските пирамиди, дори и Тадж Махал
•    Как това пропорционално разпределение се отразява на визуалния ефект на сградите.

 

 

 

Природни примери:

•    Как природата използва Златното сечение в структурите и формите си.
•    Примери от растения, животни и геологични образувания.

 

 

 

 

Технологични и научни приложения:

•    Как Златното сечение се използва в съвременни технологии и научни изследвания.
•    Съвременната наука смята, златното сечение като “асиметрична симетрия”

 

Златното сечение в Графичния дизайн

 

За да бъде въприеман един дизайн на подсъзнателно ниво, всички елементи е необходимо да следват определена последователност. Рекламните материали, плакатите, кориците на книги и визитните картинки и не са просто картинки и и текстове. Те са успешно подредени елементи снимки, графики, изображения и текстове. А един изчистен и подреден дизайн винаги постига целта си да достигне до правилната аудотория много по-лесно и качествено. 

 

 

Златното сечение в Уебдизайна 

 

 

Ден на Фибоначи 23 ноември 2023 

Малко хора знаят, че има Ден на Фибоначи. Датата, на която се почита днес, не е случайна, а съответства на първите числа в редицата на Фибоначи - 1 1 2 3. 

Фибоначи не е първият, който се е сетил за тази последователност на числата, но той е първият, който я е донесъл в европейския свят и е наясно с нейното значение за прогреса на науката. 

 

Поредицата от числа е свързана със „златното число“ и „златния триъгълник“, които от своя страна се повтарят в природата.

 

5 забавни факта по случай Денят на Фибоначи

1. Той е бил велик математически тълкувател

 

Точното място на раждане на Фибоначи е мистерия (подобно на по-голямата част от детския му живот), но той вероятно е роден близо до Пиза, Италия, около 1170 г. (оттук и псевдонимът му Леонардо от Пиза). Баща му, Гулиелмо, е заможен италиански търговец, митнически служител и директор на търговски пункт в Бугия, сега наречена Беджая, средиземноморско пристанище в североизточен Алжир. За съжаление малко се знае за майката на Фибоначи, която почива, ощще когато той е бил на девет години.

Тази мраморна статуя на Леонардо да Пиза, намираща се в Пиза, Италия, е завършена от Джовани Паганучи през 1863 г. Вероятно тази статуя е концепция на художник за Фибоначи, тъй като малко се знае за външния му вид. Изображение от Hans-Peter Postel и лицензирано под CC BY 2.5, чрез Wikimedia Commons.

 

 

Фибоначи е получил образованието си в Бугия, където за първи път научава за индуско-арабската цифрова система. Той скоро осъзна, че аритметиката с индуски-арабски цифри е много по-проста и по-ефективна, отколкото с римски цифри. 

 

По-късно, през 1202 г., той публикува своите открития в едно от най-популярните си произведения, Liber Abaci, което популяризира индуистко-арабските цифри в Европа. Той публикува разширено издание на това произведение през 1228 г., което е версията, с която сме запознати днес. 

 

 

Другите му публикувани произведения включват Practica Geometriae („Практиката на геометрията“) и Liber Quadratorum („Книгата на квадрата“). Благодарение на тези произведения става ясно, че Леонардо има истински талант да обяснява математически концепции.

 

 

2. Той е бил забравен в продължение на 400 години

 

По време на живота си Фибоначи израства до много уважаван и известен математик. В Италия дори го смятаха за икона. Въпреки това, след като той почива около 1240 г., името му в крайна сметка изчезва от страниците на всички писания по история на математиката.

 

Едва в края на 18-ти век името му най-накрая се появява отново. Когато чете Summa de arithmetica, geometria, correctioni et correctionalita („Обобщение на аритметиката, геометрията, пропорциите и пропорционалността“), написана от известния математик Лука Пачиоли, математикът Пиетро Косали забелязва име, което не е чувал преди.

 

Това име, както може би се досещате, е Леонардо Пизано (известен още като Фибоначи). Косали бил любопитен да научи повече за мистериозния математик. След като проучва името, Касоли осъзнава колко важна роля играе Фибоначи в разпространението на съвременната аритметика. Благодарение на Пачоли с цитирането на неговите източници, годините на анонимност на Фибоначи приключва.

 

 

3. Той не е измислил последователността на Фибоначи

 

Вярно е, че редицата на Фибоначи е кръстена на Фибоначи. Той обаче не е измислил последователността - тя всъщност е известна на индийските математици от 6-ти век.

 

Това, което той направи за последователността, беше да я популяризира, като я сподели в математическа задача в Liber Abaci. От многото текстови проблеми, представени в Liber Abaci, този проблем, известен като Проблемът със заека, привлече най-голямо внимание. Проблемът гласи:

 

„Един човек постави чифт зайци на място, оградено от всички страни със стена. Колко чифта зайци могат да бъдат произведени от тази двойка за една година, ако се предполага, че всеки месец всяка двойка ражда нова двойка, която от втория месец нататък става продуктивна?

Отговорът е 144 и за да разреши този проблем, Фибоначи използва това, което сега е известно като числата на Фибоначи или последователност на Фибоначи. Последователността на Фибоначи (0, 1, 1, 2, 3, 5, 8, 13, 21 и т.н.) е безкрайна поредица от числа, където всяко число в редицата се намира чрез събиране на двете числа преди то. Може да се опише с математическото уравнение: 

 

Fn+2 = Fn+1 + Fn.

 

 

 

Едва през 1877 г. последователността е наречена „последователността на Фибоначи“ от френския математик Едуард Лукас.

 

 

4. Liber Abaci не е преведен на английски език до 2002 г.

 

През 2002 г. Liber Abaci е преведен на английски език. Преводът е завършен от Лорънс Сиглър, професор по математика в университета Бъкнел. Когато пише книга по математика на ниво колеж, Сиглър иска да включи темата за редицата на Фибоначи. Въпреки това, когато отиде да проучи последователността, той забеляза, че по-голямата част от работата на Фибоначи никога не е била преведена на съвременен език. Сиглър бил решен да промени това.

 

След като се обучава на латински, Сиглер публикува английски превод на книгата на Леонардо, Liber Quadratorum. След това той преминава към по-интензивната задача да публикува копие на Liber Abaci на английски език. Английското издание на Liber Abaci на Sigler било публикувано посмъртно през 2002 г. Точно 800 години след публикуването на първото издание на Liber Abaci, произведението най-накрая е било достъпно на съвременен език.

 

Забележка: Преводът на Sigler на Liber Abaci се основава на повторното издание на Liber Abaci на Фибоначи от 1857 г. на математическия историк Boldassarre Boncompagni.

 

 

5. Има асоциация, посветена на числата на Фибоначи

 

Основана през 1963 г., Асоциацията на Фибоначи е специализирана в изучаването на последователности на Фибоначи и различни други свързани теми (като рекурентни отношения, комбинаторни идентичности, биномни коефициенти и прости числа). Четири пъти годишно асоциацията издава Fibonacci Quarterly, научно списание, което съдържа изследователски статии, експозитивни статии, елементарни проблеми и решения и напреднали проблеми и решения. Както подсказва името му, темите в списанието обикновено са свързани с числата на Фибоначи.

 

Смятан за велик математически тълкувател на своето време.

Източници: 

Wikipedia 

DesignBox Academy Blog 

Cosmol

 

Woman.bg 

 

 

 

Fibonacci Sequence - Последователност (Поредица, Редица) на Фибоначи

Golden Ratio - Златно Сечение

Graphic Design - Графичен Дизайн
Web Design - Уеб Дизайн

Формула на безкрайността 

 

 

 

Снимки: Unsplash, Pexels